Размещения
Мастер по семафорам
На картинках ниже изображен оптический телеграф. Такие использовались в Норвегии во время наполеоновских войн. Найдите, сколько уникальных сигналов можно передать с его помощью.
Каждая железная пластина может быть в двух состояниях: поднята и опущена.
Телеграф состоит из 6 железных пластин, каждая из которых может быть в двух состояниях: поднята и опущена. Каждый сигнал, который может передать этот семафор, можно представить как размещение с повторениями из 2 состояний пластин по 6 пластинам:
Мастер по семафорам
А вот такой замечательный семафор можно найти в Стокгольме. Сколько сигналов можно передать с его помощью?
Мастер по семафорам
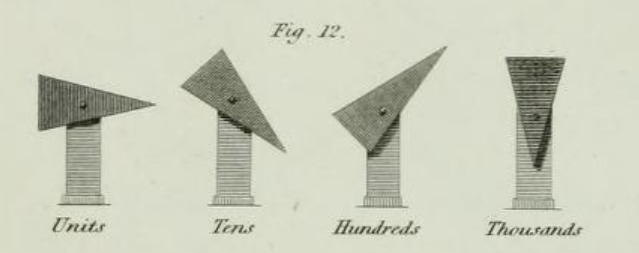
На картинке изображен концепт семафора за авторством англичанина Ричарда Лоуэлла. Он состоит из 4 вращающихся с шагом в 45 градусов треугольников. Солько сигналов можно было бы передать с помощью такого устройства?
Каждый из треугольников может быть в любом из 360 : 45 = 8 положений. Всего треугольников 4. Тогда каждый сигнал этого семафора может быть представлен как размещение с повторениями из 8 возможных положений по 4 треугольникам:
Напряженный экзамен
Пятеро студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что все студенты экзамен сдали (получили отметку 3, 4 или 5)?
Возможные варианты расставить отметки студентам можно представить как размещения с повторениями из 3 отметок по 5 студентам:
Мелочь есть? А если найду?!
Сколькими способами можно разложить в два кармана десять монет различного достоинства?
Размещайте не монеты по карманам, а карманы по монетам.
При решении этой задачи может возникнуть вполне естественное желание пытаться разместить монеты по карманам. Но это тупиковый вариант.
На самом деле размещать надо не монеты по карманам, а наоброт, карманы по монетам — каждой монете назначать свой карман, причем карманы могут повторяться. При таком подходе задача сводится к нахождению количества размещений с повторениями из 2 карманов по 10 монетам:
Служба доставки
Надо срочно доставить 6 посылок разным адресатам. Сколькими способами это можно сделать, если для передачи посылок можно послать четырех курьеров, и каждую посылку можно дать любому из них?
Курьер сам решает, в каком порядке доставлять данные ему посылки.
Внимательно подумайте, какие размещения надо считать: курьеров по посылкам или посылок по курьерам?
В этой задаче можно посчитать как размещения курьеров по посылкам, так и размещения посылок по курьерам. Самое интересное, что оба варианта возможны и дадут корректные результаты. Вот только под условие задачи подходит только один вариант.
Если посчитать размещения без повторений из 6 посылок по четырем курьерам, то мы выдадим каждому курьеру только по одной посылке! Из-за этого 2 посылки останутся на складе и адресаты их не получат! А в условии задачи сказано, что посылки надо доставить срочно.
Поэтому считать надо размещения с повторениями из четырех курьеров по 6 посылкам! В этом случае все посылки будут распределны между курьерами.
Большое путешествие
Из Николаева в Ольгино ведут 2 шоссе, соединенные 10 проселочными дорогами. Сколькими способами можно проехать из Николаева в Ольгино так, чтобы дорога не пересекала себя?
Найдите, сколько есть вариантов продолжить движение по достижении очередной проселочной дороги.
Из начальной точки, Николаево, есть 2 возможных пути на одно из двух шоссе.
Вне зависимости от выбранного пути мы достигаем первой проселочной дороги. В этот момент есть снова 2 возможных пути: продолжить ехать по шоссе или свернуть на проселочную дорогу.
Первый вариант сразу приводит ко второй проселочной дороге. Во втором варианте мы по проселочной дороге доезжаем до противоположного шоссе. Назад по этому шоссе вернуться не можем, потому что неизбежно возникнет пересечение. Поэтому остается только ехать по этому шоссе до второй проселочной дороги.
Вне зависимости от выбранного пути мы все равно оказались у второй проселочной дороги. Тут ситуация повторяется — снова 2 возможных пути, которые неизбежно приведут уже к 3 проселочной дороге. И так каждый раз.
Все путешествие можно представить как размещение с повторениями из 2 возможных путей по 11 «точкам выбора» (одна в начале пути и 10 на каждой из проселочных дорог):
Встречное движение
Пусть при том же условии из задачи «Большое путешествие» два путешественника выезжают из Николаева по разным шоссе. Сколькими способами может произойти путешествие так, что ни один участок шоссе они не проезжают в одном и том же направлении?
Покажите, что количество возможных путей на каждом выборе не поменяется.
Теперь у нас уже два человека. Значит ли это, что на каждом перекрестке появляется больше вариантов пути? Нет.
Дело в том, что абсолютно на каждом перекрестке они должны делать одинаковый выбор. Первый сворачивает на проселочную дорогу — второй обязан свернуть на нее же. Первый продолжает ехать по шоссе — второй поступает так же.
Если хоть раз они выберут разные действия, то один из них неизбежно попадет на то же самое шоссе, на котором находится воторой и пройдет тот же участок и в том же направлении.
Значит, по достижении каждой из 10 проселочных дорог совместное путешествие обоих человек может быть продолжено только 2 способами:
Самого первого выбора (выбора шоссе) тут нет, так как по условию они уже совершили этот выбор.
Последнее путешествие
Из Ольгино в Пеньки ведут 3 шоссе, пересекаемые 4 проселочными дорогами. Сколькими способами можно совершить путешествие, если ни по одному участку шоссе не едут в направлении Ольгино и ни один участок не проезжают дважды?
Найдите, сколько есть вариантов продолжить движение по достижении очередной проселочной дороги.
Стартовое шоссе можно выбрать 3-мя способами.
Вне зависимости от выбранного шоссе, когда путешественник доедет до первой проселочной дороги, у него будет 3 варианта продолжить путь:
Продолжить движение по шоссе до второй проселочной дороги
Свернуть на проселочную дорогу, доехать до центрального шоссе, свернуть на него и доехать до второй проселочной дороги
Свернуть на проселочную дорогу, доехать до противоположного шоссе (минуя центральное), свернуть на него и доехать до второгой проселочной дороги
Такая ситуация будет происходить на каждой из 4 встречающихся проселочных дорог. Итого всего 1 + 4 = 5 выборов, в каждом из которых можно выбрать один из 3 вариантов:
Нулевая буква
Алексей хочет посчитать сколько однобуквенных, двухбуквенных и трехбуквенных слов можно составить из букв A, B, C, D. Чтобы одним ходом посчитать сразу все слова, он добавил к буквам особый элемент — нулевую букву . Она означает пустоту — отсутствие буквы.
Количество сразу всех однобуквенных, двухбуквенных и трехбуквенных теперь можно представить как размещения с повторениями из 5 букв (4 буквы и одна нулевая) по 3 «вакантым местам» в слове:
Правильно ли поступил Алексей? Если нет, объясните, в чем ошибка в его подходе и найдите правильное количество слов.
Проблема в том, что размещения это упорядоченные комбинации.
Идея добавить нулевую букву отличная и она даже работает, но не в формуле размещений. Размещение по определению — упорядоченная комбинация, то есть порядок расположения элементов в ней имеет значение.
Приведем пример. Вот несколько комбинаций, которые идут в зачет в формуле :
Все эти три разных размещения обозначают одно и то же однобуквенное слово A. Поэтому, среди 125 полученных слов есть много вот таких вот дубликатов с разным положением нулевых букв.
Для получения правильного ответа надо убрать нулевую букву и отдельно посчитать сначало количество однобуквенных слов, потом двухбуквенных, а затем и трехбуквенных.
Получили три непересекающихся групп слов. Используя правило суммы находим все возможные слова:
Алексей не учел, что размещения это упорядоченные комбинации. Из-за этого в его ответе много дубликатов. Правильное количество слов — 84.
Старые автомобильные номера
Когда-то автомобильные номера состояли из одной, двух или трех букв и следующих за ними четырех цифр. Найдите число таких номеров, если использовались 32 буквы.
Отдельно посчитайте количество комбинаций из букв, отдельно количество комбинаций из цифр. Потом используйте правило умножения.
По отдельности найдем количество всех однобуквенных, двухбуквенных и трехбуквенных слов, которые можно составить из 32 букв:
Получили три непересекающихся групп слов. Используя правило суммы находим все возможные слова:
Теперь разбираемся с цифрами. Всего их 10, а в номере можно записать только 4. Количество всех таких комбинаций цифр можно найти по формуле размещений с повторениями из 10 цифр по 4 местам:
Итак, у нас есть возможных комбинаций букв. Вне зависимости от выбранной комбинации букв, затем есть еще способов выбрать набор цифр. Находим число всех возможных автомобильных номеров по правилу умножения:
Всего больше 338 миллионов номеров!
Новые автомобильные номера
В 2004 году в России давали автомобильные номера типа , в которых употреблялись цифры и кирилические буквы, имеющие аналог в латинском алфавите (таких 12). Первые два элемента — цифры (код региона), затем идет буква, затем трехзначное число и под конец еще две буквы.
Сколько таких автомобильных номеров могли выдать в России? А сколько номеров могли выдать в Москве, на которую выделили три кода региона: 77, 97 и 99?
Для удобства сначала найдите количество номеров на каждый регион.
Посчитаем сначала, сколько всего может быть буквенных комбинаций. Каждую такую комбинацию можно представить как размещение с повторениями из 12 букв по 3 местам:
Таким же образом находим количество комбинаций из трех цифр между буквами:
Выбор комбинации букв никак не влияет на выбор комбинации цифр, поэтому можно применить правило умножения.
Мы нашли количество автомобильных номеров на один регион. Теперь можно ответить на оба поставленных в задаче вопроса. Стоит только учесть, что региона с кодом 00 в России не существует, поэтому всего регионов 99, а не 100.
Все возможные номера в России:
Из них выделено для Москвы:
Всего возможных номеров в России:
Из них выделено для Москвы:
Скажите «Ааа»
В некотором государстве не было двух жителей с одинаковым набором зубов. Какова может быть наибольшая численность населения этого государства?
Во рту человека не может быть более 32 зубов.
Каждое «вакантное место» в челюсти может иметь одно из двух состояний: «зуб есть» и «зуба нет».
У каждого жителя в этом государстве свой набор, своя уникальная комбинация зубов. Какие-то есть, какие-то отсутствуют. Каждую такую комбинацию можно представить как размещение с повторениями из 2 состояний («есть зуб» и «нет зуба») по 32 местам в челюсти:
Конструктор чисел
Сколько чисел, меньших миллиона, можно написать с помощью цифр:
8 и 9;
7, 8, 9;
0, 8, 9 (с цифры 0 число начинаться не может)?
Отдельно с помощью формулы размещений с повторениями посчитайте количество однозначных, двузначных, ..., шестизначных чисел, а потом найдите общее их количество по правилу суммы.
Отдельно с помощью формулы размещений с повторениями считаем количество однозначных, двузначных, ..., шестизначных чисел, а потом находим общее их количество по правилу суммы.
Первый вариант:
Второй вариант:
Третий вариант. Первая цифра в числе не может быть 0, поэтому в каждой группе будет 2 варианта выбрать первую цифру, а затем уже по 3 варианта на каждую следующую цифру:
126
1092
726
Найди работу
Трое юношей и две девушки выбирают себе место работы. В городе есть три завода, где требуются рабочие (туда берут лишь мужчин), два магазина, куда берут лишь женщин, и две фирмы, куда требуются и мужчины, и женщины. Сколькими способами они могут распределиться между этими предприятиями?
Отдельно найдите количество способов устроить на работу только мужчин, потом только женщин.
Задача пытается нас запутать, подталкивая работать сразу и с юношами, и с девушками.
Разберемся сначала только с юношами. Их всего три и каждый может устроиться на любую из 5 работ (3 завода и 2 фирмы). Количество всех способов устроить каждого мужчину на работу находим по формуле размещений с повторениями из 5 мест для работы по 3 юношам:
Точно также поступаем и с девушками:
Итак, есть 125 способов устроить на работу мужчин. Вне зависимости от того, на какие работы устроились мужчины, есть еще 16 способов устроить на работу женщин. По правилу произведения находим общее количество способов устроить каждого на работу:
Пернатая братва
Имеется три курицы, четыре утки и два гуся. Сколькими способами можно выбрать из них несколько птиц так, чтобы среди выбранных оказались и куры, и утки, и гуси?
Каждой птице (например, курице) можно назначить состояние «выбрана» и «не выбрана». Используйте этот факт, чтобы посчитать количество способов выбрать птиц этого типа.
Разберемся сначала с курицами. Каждой курице можно назначить состояние «выбрана» и «не выбрана». Тогда каждый способ выбрать куриц можно представить как размещение с повторениями из 2 состояний по 3 курицам:
Но так как хотя бы одна курица должна быть выбрана обязательно, комбинацию из трех состояний «не выбрана» мы убираем. Всего 7 варинатов выбрать куриц.
Точно так же находим все способы выбрать уток и гусей:
Итак, есть 7 способов выбрать куриц. Вне зависимости от сделанного выбора потом есть 15 способов выбрать уток и 3 способа выбрать гусей. Используем правило произведения:
Светофорные огни
На перекрестке имеется m светофоров. Сколько может быть различных состояний этих светофоров, если каждый светофор независимо от остальных имеет три возможных состояния: горит зеленый; горит желтый; горит красный?
Решите ту же задачу, если допускаются все возможные комбинации огней каждого светафора.
Для подсчета количества состояний, в которых может быть один светофор, используйте тот факт, что каждый его цвет может иметь состояние «включен» или «выключен».
Каждый светофор может быть в одном из трех состояний. Всего светофоров m. Каждое состояние всех светофоров может быть представлено как размещение из 3 состояний по m светофорам:
Если допускаются все возможные комбинации огней, то надо сначала посчитать, сколько их всего. Каждый светофор имеет три цвета. Каждый цвет может быть в двух состояниях: «включен» или «выключен». Тогда любая комбинация огней одного светофора может быть представлена как размещение с повторениями из 2 состояний по 3 цветам:
При таких условиях все светофоры могут находиться не в состояниях, а в состояниях.
С тремя состояниями все светофоры могут находиться в состояниях. Если ограничений на состояние светофоров нет, то все они могут находиться в состояниях.
Без «А» никудА
Сколько можно составить из 32 букв шестибуквенных слов, содержащих хотя бы один раз букву «а»?
Представьте ответ как разность двух формул количества размещений с повторениями.
Количество шестибуквенных слов, которые можно набрать из 32 букв равно . Но среди этих слов есть и те, в которых совсем нет буквы «а». Раз в таких словах нет буквы «а», то можно сказать, что они составлены не из 32 букв, а из 31.
Слов без буквы «а», то есть слов из 31 букв всего . Для получения ответа надо вычесть из всех слов те, в которых совсем нет буквы «а»:
Однобуквенные близнецы
В селении проживает 1000 жителей. Докажите, что по крайней мере двое из них имеют одинаковые инициалы.
Найдите количество возможных инициалов.
Инициалы человека это первые буквы его имени и отчества. Так как имя и отчество точно не могут начинаться с букв «Ь» и «Ъ», то всего есть 33 - 2 = 31 буква. Каждые инициалы можно представить как размещение с повторением из 31 буквы по 2 местам:
Видим, что уникальных инициалов хватит всего на 961 человек. А в селении проживает 1000 жителей. Это означает, что в нем точно найдется по крайней мере два человека с одинаковыми инициалами.
Телефонный номер
Сколько существует семизначных телефонных номеров, в первых 3 цифрах которых не встречаются цифры 0 и 9?
Отдельно посчитайте количество комбинаций первых трех цифр в номере, а потом количество комбинаций оставшихся четырех цифр.
Найдем количество вариантов выбрать первые три цифры телефонного номера. В них можно использовать только 8 цифр:
Теперь найдем количество вариантов выбрать оствшиеся четыре цифры, на которых уже нет никаких ограничений:
Выбор первых трех цифр никак не влияет на выбор оставшихся четырех. Поэтому можно использовать правило произведения:
Власть имущие
В правление избрано 9 человек. Из них надо выбрать председателя, заместителя председателя и секретаря. Сколькими способами это можно сделать?
Восползуйтесь формулой размещений без повторений.
Каждый вариант избрать трех членов правления можно представить как размещение без повторений из 9 человек по 3 должностям:
Власть имущие
Имеется {{{ gloves }}} пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну — на правую руку так, чтобы эти перчатки были различных размеров?
{{{ answer }}}
Несинхронный переводчик
Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из пяти языков: русского, английского, французского, немецкого, итальянского на любой другой из этих пяти языков? На сколько больше словарей придется издать, если число различных языков равно 10?
Словарь нужен на каждую пару языков. Например: русско-английский словарь, французско-немецкий и так далее.
Составим все возможные пары языков, между которыми может выполняться перевод. Каждая такая пара может быть представлена как размещение без повторений из 5 языков с которых надо перевести по 4 оставшимся языкам, на которые надо перевести:
Каждой из этих 20 пар языков требуется свой словарь. Значит, всего нужно 20 словарей.
Если языков 10, то потребуется уже словарей, что на 70 больше, чем в случае с 5 языками.
Для 5 языков нужно словарей. Если языков 10, то нужно на 70 больше словарей.
Существует ли судьба?
Докажите, что .
Объясните смысл этого равенства.
Доказывается равенство элементарно. Выпишем сначала формулу для :
Умножение на один в конце на результат никак не влияет, поэтому его можно отбросить. Но если мы его отбросим, то количество вакантных мест для размещения без повторений уменьшится на единицу: с n до . А это и будет !
Смысл равенства
В самой сути размещения без повторений лежит правило произведения. На первое вакантное место мы можем поместить n элементов, на второе элементов и так далее.
На вакантное место под номером у нас остается в запасе всего 2 элемента. Поместив на это место один из них, оставшийся последний элемент автоматом попадает на место n. Мы его даже не выбираем, его судьба определяется еще на месте.
Раз элемент для места n не дает никаких разветвлений, а определяется уже на месте, то и формула дает тот же результат, что и формула .
Родовые апельсины
У отца есть 5 различных апельсинов, которые он дает своим 8 сыновьям, причем каждый получает или один апельсин, или ничего. Сколькими способами это можно сделать? А если число апельсинов, получаемых каждым сыном, не ограничено? Как изменится ответ, если отец должен раздать все пять апельсинов?
Используйте размещения из сыновей по апельсинам.
К этой задаче есть два подхода. В более простом подходе отец обязательно раздает все пять апельсинов. В более сложном подходе отец не обязательно отдает все апельсины.
Отец отдает все апельсины
Если отец точно отдает все апельсины, то нам достаточно выписать все размещения без повторений из 8 сыновей по 5 апельсинам.
Если число апельсинов, получаемых каждым сыном, не ограничено, то вместо размещения без повторений используем размещения с повторениями:
Отец может отдать не все апельсины
В этой ситуации нам надо отдельно рассчитать все способы отдать только 1 апельсин, только 2 и так далее. Потом объединить все эти способы с помощью правила суммы.
Отец может решить не отдавать апельсины вообще. Это первый способ.
Отец может решить отдать только один апельсин. Сделать это он может способами если у каждого сына не может быть больше одного апельсина и , есть ограничений нет. Объединяем с предыдущим результатом:
Отец может решить отдать только два апельсина. Сделать это он может способами если у каждого сына не может быть больше одного апельсина и , есть ограничений нет. Объединяем с предыдущим результатом:
Ну и так далее вплоть до пяти апельсинов:
Отец отдает все апельсины. У каждого сына не более 1 апельсина:
Отец отдает все апельсины. Ограничений на количество апесинов у сыновей нет:
Отец может отдать не все апельсины. У каждого сына не более 1 апельсина:
Отец может отдать не все апельсины. Ограничений на количество апесинов у сыновей нет:
День студента
В комнате студенческого общежития живут трое студентов. У них есть 4 чашки, 5 блюдец и 6 чайных ложек (все чашки, блюдца и ложки отличаются друг от друга). Сколькими способами они могут накрыть стол для чаепития (каждый получает чашку, блюдце и ложку)?
Отдельно посчитайте, сколькими способами можно выдать каждый элемент посуды.
Разберемся с каждым типом посуды отдельно. Каждый способ раздать чашки можно представить как размещение без повторений из 4 чашек по 3 студентам:
Точно так же считаем количество способов раздать блюдца и чайные ложки:
Итак, выдать чашки можно 24 способами. Вне зависимости от выбранного способа выдать чашки, потом есть еще 60 способов выдать блюдца и 120 способов выдать чайные ложки. Применяем правило произведения:
Остатся только один
В соревновании по гимнастике участвуют 10 человек. Трое судей должны независимо друг от друга пронумеровать их в порядке, отражающем их выступление в соревновании. Победителем считается тот, кого назовут первым хотя бы двое судей. В скольких случаях победитель соревнований будет определен?
Проще найти не количество совпадений в решениях судей относительно первого места, а варианты, когда они все выбрали разных гимнастов на первое место.
Найдем, сколькими способами судьи могут выбрать участников на первое место. Каждый такой способ можно представить как размещение с повторениями из 10 участников по первым местам в списках 3 судей:
Искать совпадения решений трех или двух судей довольно сложно. Вместо этого найдем все варианты, когда судьи отдали первое место разным гимнастам. Каждый такой вариант можно представить как размещение без повторений из 10 гимнастов по 3 судьям:
Всего назначить первые места можно 1000 способами, из них 720 вариантов, где все судьи выбрали разных гимнастов. Тогда остается 1000 - 720 = 280 вариантов, когда как минимум двое судей сошлись во мнениях относительно первого места.
Страсти по масти
Сколькими способами можно выбрать из полной колоды карт, содержащей 52 карты, по одной карте каждой масти? А если среди вынутых карт нет ни одной пары одинаковых, т.е. двух королей, двух десяток и т.д.?
В каждой масти есть по 13 карт.
На каждую из четырех мастей приходится по 13 карт. Тогда каждый способ выбрать по одной карте каждой масти можно представить как размещение с повторениями из 13 карт каждой масти по 4 соответствующим мастям:
А если не должно быть одинаковых карт, то, вынув карту первой масти, мы тем самым оставляем только 12 вариантов вынуть карту второй масти и так далее. Это уже размещения без повторений:
способов выбрать 4 карты разных мастей и способов выбрать их без повторений.
Чудо-счетчик
Найдите сумму всех трехзначных чисел, которые можно написать с помощью цифр 1, 2, 3, 4. А если никакая цифра не должна появляться дважды в записи каждого числа?
По отдельности найдите сумму всех единиц, всех десятков и всех сотен в составе этих трехзначных чисел.
Любые трехзначные числа, например 423 и 122, можно записать в развернутом виде:
Вместо того, чтобы складывать числа напрямую, можно по отдельности сложить их единицы, их десятки и их сотни.
Тогда задача сводится к поиску суммы всех единиц, всех десятков и всех сотен в составе этих трехзначных чисел.
С повторениями
Давайте посчитаем, сколько трехзначных чисел имеют в разряде единиц цифру 1, или, другими словами, заканчиваются на цифру 1. Если разряд единиц менять нельзя, то остаются только размещения с повторениями из 4 цифр по 2 оставшимся разрядам: десяткам и сотням.
Всего 16 трехзначных чисел, которые заканчиваются на 1. Но еще 16, которые заканчиваются на 2. Столько же и для 3 и для 4 на конце.
Найдем сумму единиц всех этих трехзначных чисел, то есть сумму 16 единиц, 16 двоек, 16 троек и 16 четверок:
Точно такая же история и с разрядом десятков. Есть 16 чисел, у которых в разряде десятков стоит цифра 1, 16 чисел с цифрой 2 и так далее. Найдем сумму десятков всех этих трехзначных чисел, то есть сумму 16 десяток, 16 двадцаток и так далее:
Наконец, по такой же схеме найдем сумму сотен всех этих трехзначных чисел:
Мы по отдельности нашли сумму всех единиц, всех десятков и всех сотен в составе этих трехзначных чисел. Теперь сложим все это друг с другом и получим искомую сумму всех чисел:
Без повторений
Если никакая цифра не должна появляться дважды в записи трехзначного числа, то вместо размещений с повторениями надо использовать размещения без повторений, причем уже из 3 цифр, потому что одну мы уже зафиксировали.
Например, если зафиксировали разряд единиц, то формула такая:
Ну и повторяем все те же самые действия:
Сумма всех чисел:
Сумма всех трехзначных чисел равна . Если одинаковых цифр нет, то сумма равна 6660.
Разные кости судьбы
Сколькими способами могут выпасть три различные игральные кости? Во скольких случаях хотя бы на одной кости выпадет 6 очков? Во скольких случаях ровно на одной кости выпадет 6 очков? Во скольких случаях ровно на одной кости выпадет 6 очков, а на другой — 3 очка?
Пользуйтесь размещениями с повторениями, без повторений и правилом умножения.
Каждая из 3 костей может упасть на одну из 6 сторон. Каждый способ выпадания трех костей можно представить как размещение с повторениями из 6 возможных выпавших сторон по 3 костям. Находим количество этих размещений по формуле:
Варианты выпадения не менее одной шестерки можно получить, если из всех возможных вариантов вычесть варианты, когда шестерка точно не выпадает:
Для выпадения ровно одной шестерки сначала 3-мя способами выбираем кость, на которой выпадет шестерка. Вне зависимости от выбранной кости оставшиеся две могут выпасть способами. Используем правило умножения:
Для выпадения ровно одной шестерки и тройки сначала выберем пару костей, на которых выпадет 6 и 3. Для этого «разместим» числа 6 и 3 без повторений по 3 костям: . Вне зависимости выбора двух костей, на оставшейся третьей кости может выпасть 4 возможных стороны. Используем правило умножения:
Варианты выпадения трех костей:
Если есть хотя бы одна кость с 6 очками:
Если есть ровно одна кость с 6 очками:
Если на одной кости ровно 6 очков, а на другой 2:
Превосходство четырех
Сколько различных четырехзначных чисел, делящихся на 4, можно составить из цифр 1,2,3,4,5, если каждая цифра может встречаться несколько раз? А если каждая цифра встречается лишь один раз?
Число делится на 4, если его последние две цифры образуют число, которое делится на 4.
В первых двух разрядах можно поместить любые цифры:
Последние две цифры должны образовать число, которое делится на 4. Найдем все такие числа прямым перебором. Фиксируем первую цифру и перебираем вторую:
Всего 5 способов завершить число. Используем правило проиведения:
Если цифры не могут повторяться, то надо зайти с другой стороны. Всего есть 4 способа выбрать последние две цифры (кроме 44). Но тогда две цифры уже заняты, поэтому на место первых двух цифр остается разместить три оставшиеся без повторений:
Если цифры могут повторяться: .
Если не могут:
Композиция числа
Сколькими способами можно разложить число n на слагаемые?
Например, число 3 имеет 4 композиции:
Порядок слагаемых имеет значение!
Представьте число n как сумму n единиц. Подумайте, на что можно заменить плюсы в этой сумме.
Самый длинный способ записать число n — представить его в виде суммы n единиц:
Заменим теперь в этой записи все плюсы на пустые квадраты. Всего этих пустых квадратов , на единицу меньше, чем количество единиц:
В каждый из этих квадратов можно вписать либо (+), либо запятую (,). Каждое заполнение всех квадратов даст в результате очередное разложение числа. Например:
Итак, каждое разложение числа n на слагаемые можно представить как размещение с повторением из двух символов (плюса и запятой) по квадратам:
Как видите, задача о нахождении количества композиций любого числа решается довольно просто. Но у этой задачи есть злобный брат-близнец — задача о разбиении числа. Это почти то же самое, вот только порядок слагаемых значения не имеет.
Например, число 3 имеет 4 композиции, но только 3 разбиения:
Казалось бы, если для нахождения композиций есть простая формула, то и разбиения должны находиться примерно так же элементарно. К сожалению, это не так. До сих пор не найдено явной формулы для количества разбиений и неизвестно, есть ли она вообще! Были найдены асимпотитические формулы. Их получили математики Годфри Харди и Сриниваса Рамануджан.
Поразительно, как одна задача имеет элементарное решение, а вторая, практичеки идентичная первой, явного решения не имеет вовсе.
Про удивительную жизнь Рамануджана снят отличный фильм — «Человек, который познал бесконечность». В нем есть сцены, где оба математика занимаются выводом и доказательством формул количества разбиений.
В некоторых телефонах на Android вместо пинкода из цифр можно задать пальцем рисунок для разблокировки. Сколькими способами можно задать этот рисунок?
Например, когда дается количество размещений и k, а просят найти n и так далее. Тут легко их сделать генерирующимися.