Прямой перебор

Простой, безотказный и в то же время самый медленный способ решать задачи. Но если до него все же дошло дело, надо уметь перебирать комбинации так, чтобы не запутаться.

Зачем это нужно?

Очень многие комбинаторные задачи можно решить просто вручную составив все возможные комбинации.

Зачем вообще проходить эту тему?
Перебрать варианты любой ведь сможет!
Мы ведь и зашли в этот учебник, чтобы изучать приемы быстрого решения!

Эти и подобные вопросы и возмущения понятны. Но прежде чем научиться летать, нужно сначала научиться ползать. Прежде чем узнать о хитрых приемах, надо сначала изучить и отработать базу — перебор вариантов вручную.

Не волнуйтесь, у прямого перебора вариантов тоже есть свои хитрые приемы и весьма интересные задачи. Скучно не будет.

Перебираем с умом

Казалось бы, что может быть проще!? Просто берешь и выписываешь все возможные комбинации! Как-бы да, но при бездумном и бессистемном выписывании очень легко можно пропустить какую-то комбинацию. Или посчитать одну и ту же дважды. Чтобы такого не проиходило, нужно придерживаться двух простых правил:

Правила перебора

Каждому элементу дать уникальное и короткое обозначение.
Придумать удобный алгоритм перебора и строго ему следовать.

Уникальные обозначения элементам нужно давать, чтобы не держать в голове сложные сущности. Превратить их в что-то простое — буквы или символы. Именно так сущности вроде «яблок» и «апельсинов» и «бананов» во время решения задачи превращаются в обезличенные буквы «я», «а» и «б».

Алгоритм перебора помогает не запутаться, не пропустить комбинации и не посчитать лишние. При правильном выборе алгоритма решение задачи на перебор из пытки превращается вы повторение четких действий, которое неизбежно приведет к правильным результатам.

На словах правила звучат довольно просто. Теперь научимся применять их для решения задач. Начнем с чего-нибудь простого:

Насыщенный день

Петр должен убраться в комнате, сделать домашнее задание и поработать над личным проектом. Сделать нужно все, но Петр еще не решил, в какой последовательности. Сколькими способами он может выбрать эту последовательность?

Решение

Обозначим уборку в комнате буквой «У», домашнее задание буквой «Д», а работу над личным проектом буквой «П». Введя эти обозначения мы выполнили первый пункт правил перебора.

Перебирать будем так: сначала разберем варианты, когда буква «У» стоит первой, потом второй, затем последней. Введя такой порядок мы выполнили второй пункт правил перебора. Приступаем:

\bm{У}\text{ДП} \quad \bm{У}\text{ПД} \\ \text{Д}\bm{У}\text{П} \quad \text{П}\bm{У}\text{Д} \\ \text{ДП}\bm{У} \quad \text{ПД}\bm{У}

Всего 6 способов распланировать 3 дела на день.

Предложенный выше алгоритм через фиксацию буквы может подойти не всем. Кому-то удобнее записывать варианты в алфавитном порядке. Делайте так, как удобно вам. Главное — строго придерживайтесь выбранного алгоритма!

В некоторых задачах предстоит работать с числами и цифрами. Они и так записываются коротко и хорошо друг от друга отличаются. Поэтому им, обычно, не нужно придумывать уникальные обозначения и первое правило перебора можно считать автоматически выполненным.

В поисках чисел

Сколько существует четырехзначных чисел, сумма цифр которых меньше 4?

Решение

Мы работаем с числами, поэтому уникальные обозначения вводить не надо. Но все еще нужно выполнить второе правило перебора — придумать удобный алгоритм.

Чтобы не запутаться, не потерять и лишний раз не засчитать числа, будем указывать их в порядке возрастания: от маленьких к большим. То есть каждое следующее число должно быть больше предыдущего. И помним, что сумма цифр в числе должна быть меньше 4, то есть равна 1, 2 или 3.

1000, \ 1001, \ 1002, \ 1010, \ 1011, \ 1020, \ 1100, \ 1101, \ 1110, \ 1200, \\ 2000, \ 2001, \ 2010, \ 2100, \\ 3000

Будем честны, предыдущие примеры вполне можно было решить без всяких правил, просто наобум перебирая дела и числа. Да, это было бы дольше и не так удобно, но все же возможно. Рассмотрим теперь пример задачи, которую без правил перебора решить, скорее всего, не выйдет.

Задача Эйлера о шляпах

Ресторан посетили 4 человека. Свои шляпы они отдали швейцару. На выходе невнимательный швейцар раздал шляпы случайным образом. Сколько существует вариантов, когда каждый гость получил чужую шляпу?

Решение

Дадим каждому человеку свой номер от 1 до 4. Каждой шляпе тоже дадим номер. Причем номер шляпы совпадает с номером ее владельца. Шляпа 3 принадлежит гостю 3 и так далее.

Дальше придумаем, как удобно обозначать варианты выдачи шляп. Будем записывать их в виде набора из четырех цифр, причем позиция цифры означает человека, а сама цифра номер шляпы. Например, набор 1234 означает, что каждый человек получил свою шляпу. А набор 1243 означает, что третий человек получил шляпу четвертого, а четвертый шляпу третьего:

\overset{1\text{ч}}{1} \ \overset{2\text{ч}}{2} \ \overset{3\text{ч}}{4} \ \overset{4\text{ч}}{3}

Мы свели задачу к тому, что нужно просто найти все наборы из четырех цифр, в которых позиция каждой цифры не равна самой цифре.

Введя подобные обозначения, мы выполнили первое правило прямого перебора. Но как не запутаться и перечислить все такие наборы цифр? Для этого надо придумать грамотный алгоритм перебора (2-е правило перебора).

Построим таблицу, в верхней строчке которой укажем номера гостей. Потом добавляем строки с четырехзначными числами в порядке возрастания. Следим за тем, чтобы номер шляпы не совпал с номером человека. Такие варианты вычеркиваем:

\def\arraystretch{1.5} \begin{array}{cccc} 1\text{ч} & 2\text{ч} & 3\text{ч} & 4\text{ч} \\ \hline \color{red} 2 & \color{red} 1 & \color{red} 3 & \fcolorbox{red}{transparent}{\color{red}4} \\ 2 & 1 & 4 & 3 \\ \color{red} 2 & \color{red} 3 & \color{red} 1 & \fcolorbox{red}{transparent}{\color{red}4} \\ 2 & 3 & 4 & 1 \\ 2 & 4 & 1 & 3 \\ \color{red} 2 & \color{red} 4 & \fcolorbox{red}{transparent}{\color{red}3} & \color{red} 1 \end{array}

Красным цветом помечены неподходящие варианты, то есть когда гость получил свою шляпу. В красную рамочку взяты номера шляп, которые попали в руки своих владельцев.

Продолжая в том же духе, после вычеркивания всех лишних наборов, останется таблица во всеми нужными нам вариантами раздачи шляп:

\def\arraystretch{1.5} \begin{array}{cccc} 1\text{ч} & 2\text{ч} & 3\text{ч} & 4\text{ч} \\ \hline 2 & 1 & 4 & 3 \\ 2 & 3 & 4 & 1 \\ 2 & 4 & 1 & 3 \\ \hline 3 & 1 & 4 & 2 \\ 3 & 4 & 1 & 2 \\ 3 & 4 & 2 & 1 \\ \hline 4 & 1 & 2 & 3 \\ 4 & 3 & 1 & 2 \\ 4 & 3 & 2 & 1 \end{array}

Получаем всего 9 вариантов, когда каждый гость получил чужую шляпу.

Заметили, что самое сложное в таких задачах — как раз таки выполнить два правила: ввести обозначения и придумать алгоритм? Но когда оба пункта правил выполнены, то думать уже не надо. Остается только аккуратно и внимательно перебирать варианты. Из всего этого следует довольно простой вывод:

Если соблюдать правила перебора, то множество комбинаторных задач можно решить полным (прямым) перебором. Скорее всего это будет долго, но правильный ответ все равно будет получен.

Дерево вариантов

В большинстве задач дать элементам уникальные обозначения (выполнить первое правило перебора) не составляет труда. Проблемы возникают на втором шаге — придумывании алгоритма перебора. Порой ну никак не получается нащупать удобный механизм.

Тут главное не отчаиваться, ведь существует универсальный, удобный, наглядный и безотказный механизм, который носит гордое название «дерево вариантов».

Дерево вариантов — универсальный алгоритм построения и перебора комбинаций.

Как там говорят? Любой человек должен создать семью, построить дом и посадить дерево? Не знаю, что там насчет первых пунктов, но дерево мы с вами сейчас посадим.

Построение дерева

В первом примере этой статьи мы искали все способы составить расписание на день. Каждое дело обозначили своей буквой: уборка — «У», домашнее задание — «Д», личный проект — «П». Таким образом, задача свелась к поиску всех способов записать друг за другом три буквы: «У», «Д» и «П». Найдем все эти способоы с помощью дерева вариантов.

Рисуем точку. Это семечко нашего дерева, его стартовый или нулевой узел. На первое место в комбинациях мы можем поставить любую из трех букв. Поэтому из стартового узла «вырастают» три ветки первого уровня. Три ветки — три буквы:

Левая ветка у нас отвечает за букву «У». После этой буквы можно записать «Д» или «П», получая комбинации «УД» и «УП». Чтобы отобразить это на дереве вариантов, из узла, на котором завершается «У», рисуем еще две ветки для букв «Д» и «П»:

То же самое происходит и с оставшимимся ветками первого уровня. Из каждой из них тоже вырастают еще по две ветки второго уровня с нужными буквами:

Сейчас на древе у нас изображены все возможные комбинации двух букв (слева направо): «УД», «УП», «ДУ», «ДП», «ПУ», «ПД». Осталось только каждой из комбинаций добавить третью букву. Причем для каждой из них эта буква всего одна.

Единственный способ завершить комбинацию «УД», это добавить к ней букву «П», чтобы получить «УДП». И так со всеми остальными комбинациями. Чтобы отобразить это на дереве, из каждого узла второго уровня вырастает одна ветка третьего уровня с соответствующей буквой:

Дерево вариантов готово! Всего у нас получилось 6 узлов последнего, третьего уровня, а значит есть всего 6 способов записать буквы «У», «Д» и «П». Рассматривая каждую ветку по отдельности от нулевого узла к третьему, мы получаем все возможные комбинации: «УДП», «УПД», «ДУП» и так далее.

Говоря о «деревьях» мы представляем себе растения, которые растут снизу вверх. Но в математике форма и внешний вид деревьев не играют никакой роли. Оно может «расти» вверх, вниз, да хоть во все стороны света. Главное, чтобы были узлы и ветки, и пофиг как они расположены, лишь бы вам было удобно.

Деревья бывают разными

Честно говоря, комбинации из трех букв можно и без деревьев найти. Теперь рассмотрим примеры, которые без деревьев решить будет весьма проблематично.

Лучшие из лучших

Для полета на Марс требуется собрать команду. На место командира есть 4 кандидата: $c_1, c_2, c_3, c_4$ . На место инженера 3 кандидата: $i_1, i_2, i_3$ . На место врача тоже 3 кандидата: $v_1, v_2, v_3$ .

Проверка показала, что командир $c_1$ психологически совместим с инженерами $i_1$ и $i_3$ и врачами $v_2, v_3$ . Командир $c_2$ — с инженерами $i_1, i_2$ и всеми врачами. Командир $c_3$ — с инженерами $i_1, i_2$ и врачами $v_1, v_3$ . Командир $c_4$ — только с инженером $i_3$ и всеми врачами.

Кроме того, инженер $i_1$ психологически несовместим с врачом $v_3$ , инженер $i_2$ — с врачом $v_1$ и инженер $i_3$ — с врачом $v_2$ .

Сколькими способами при этих условиях может быть составлена команда корабля?

Решение

Обратите внимание, что в задаче уже за нас ввели уникальные обозначения для каждого кандидата. То есть первое правило прямого перебора уже выполнено. Осталось только разобраться с алгоритмом и вот тут нам на помощь приходит дерево вариантов.

Из стартового угла в разные стороны добавим четыре ветки первого уровня, по одной на каждого капитана:

Все капитаны, кроме $c_4$ , совместимы с двумя инженерами. Поэтому добавляем по две ветки второго уровня трем капитанам и одну ветку второго уровня четвертому капитану:

Осталось только добавить ветки третьего уровня, которые соответствуют врачам. Делать это надо аккуратно, учитывая психологическую совместимость. Например, к ветке $c_1, i_1$ можно добавить только одну ветку с врачом $v_2$ , так как $c_1$ несовместим с врачом $v_1$ , и оба $c_1$ и $i_1$ не совместимы с врачом $v_3$ .

Получили всего 10 узлов третьего уровня на концах своих веток. Это означает, что при данных нам условиях мы можем собрать 10 разных команд для корабля.

Помните задачу Эйлера про шляпы? Не факт, что каждый догадается построить удобную таблицу и перебирать комбинации в порядке возрастания. Ничего страшного! Именно для таких безвыходных ситуаций и нужны универсальные приемы! Попробуем использовать дерево.

Полная шляпа

Решите задачу Эйлера о шляпах с помощью дерева вариантов.

Решение

Ветки первого уровня будут означать номера шляп, которые выдаются первому человеку. Для удобства номера гостей будем записывать слева от дерева. Всего 3 ветки первого уровня, так как превому человеку можно выдать шляпы с номерами 2, 3, 4.

На втором уровне веток уже идут шляпы, выдаваемые второму гостю. Здесь не может быть ветки с номером 2, потому что ее нельзя выдать втором гостю. Более того, номер ветки не должен совпадать с номерами предыдущих веток, из которых она «растет», ведь эти шляпы уже были выданы.

Продолжаем в таком же духе строить дерево кобминаций выдачи шляп. Некоторые из веток будет невозможно продолжить. Их помечаем крестиком. В итоге получится вот такое дерево:

Всего до самого «верха» дерева «доросли» только 9 веток. Это и есть все возможные варианты выдать каждому гостю чужую шляпу!

Проблемы деревьев

Дерево вариантов — мощный универсальный способ решать комбинаторные задачи прямым перебором. Но у него есть и недостаток — оно быстро разрастается в размерах и вам может просто не хватить места, чтобы указать все возможные варианты.

Другой очевидный минус — «универсальный» вовсе не означает «лучший». Зачастую можно придумать свой алгоритм, с которым задачу получится решить гораздо быстрее. Отсюда очевидный вывод:

Экспериментируйте!

В бою все средства хороши! Придумывайте разные обозначения и алгоритмы! Используйте таблицы, деревья, ритуальные танцы с бубном, да все что угодно, чтобы упростить себе задачу перебора!

Все зависит только от вашего умения выделить главную суть задачи и подать ее так, чтобы было удобно перебирать варианты.

Прямой перебор в жизни

Может показаться, что прямой перебор это своего рода крайняя мера и последний шаг. Показатель того, что вы не справились с задачей и вынуждены просто перебирать все варианты в поисках нужного.

Но не стоит относится к нему именно так. Как раз наоборот, хорошо, что у нас есть возможность вручную проверить все комбинации. Далеко не все задачи можно раскусить, применив одну-две красивые формулы. В реальной жизни все сложнее. Об этом сейчас и поговорим.

«Бомба» Тьюринга

1941 год, в самом разгаре идет Вторая мировая война — одна из самых страшных войн в истории. Для передачи приказов и другой ценной информации Германия использует шифровальные машины «Энигма».

У этих машин было от 3 до 5 роторов, положение которых определяло печатаемый символ. После каждого введенного символа роторы вращались, из-за чего даже изначально одинаковые буквы в исходном сообщении превращались в разные буквы шифра. Чтобы расшифровать сообщение, нужно было знать, в каком именно стартовом положении были установлены роторы до начала набора.

Германия использовала «Энигму» во флоте и авиации
В верхней части машины хорошо видны роторы

Первые успехи в расшифровке «Энигмы» получили в польском «Бюро шифров» еще до начала Второй мировой. После начала войны в особняке «Блетчли-парк», секретном центре британской разведки, была запущена программа «Ультра». Ее главной задачей был перехват и расшифровка сообщений, передаваемых с помощью «Энигмы».

Уинстон Черчилль о Блетчли-парке

«Это моя курочка-ряба, которая несёт золотые яйца, но никогда не кудахчет.»

Лучшие британские математики пытались найти способ быстро расшифровывать сообщения немцев. Основным теоретиком среди них был Алан Тьюринг, «отец» современной информатики.

Итогом этой колоссальной работы стало создание машины «Бомба». Она повторяла поведение сразу 26 одновременно работающих «Энигм». Барабаны, выполняющие роль роторов, непрерывно крутились до тех пор, пока прямым перебором не находилось нужное положение всех роторов, позволяющее расшифровать сообщение.

Две «Бомбы»: реконструкция и американский вариант
С машинами работал специально обученный персонал

Другими словами, из-за невозможности перебирать варианты вручную (это слишком медленно), британцы создали машину, которая занималась прямым перебором вместо них. А название она получила из-за характерного тикающего звука, возникающего при повороте барабанов.

«Бомба» подбирает правильное положение роторов

Ежедневный шифр «Энигмы» взламывался за 20 минут

Успех британских дешифровщиков стал ценным вкладом в дело победы над нацизмом. Надёжность «Энигмы» не вызывала никаких сомнений у немецких специалистов. До самого конца войны немецкое командование искало причины утечек секретной информации где угодно, но не в том, что шифры успевали оперативно взламывать.

Брутфорс

С повсеместным распространением компьютеров, телефонов и интернета, мы стали хранить в них свою информацию. Для защиты этих данных мы используем пароли — комбинации из символов.

Слабое звено такой защиты состоит в том, что количество возможных паролей конечно, ведь это всего лишь комбинации конечной длины (как правило в районе 10 символолв) из конечного набора элементов (на телефонах это 10 цифр).

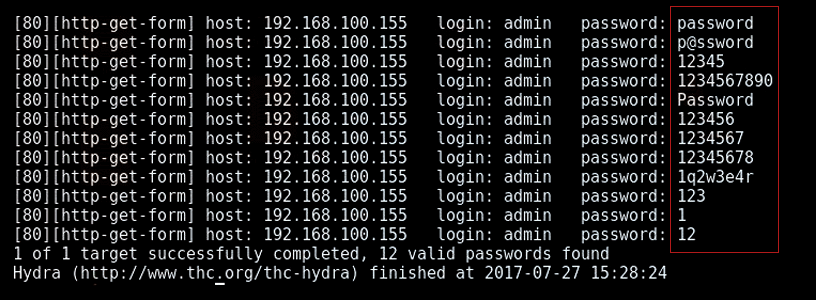
А раз паролей не бесконечное количество, то все их можно перебрать и уж какой-то точно подойдет. Делают это с помощью специальных программ, а сам процесс взлома пароля через перебор всех возможных вариантов называется брутфорс, от английского выражения «brute force» (грубая сила).

Программа завершила брутфорс и нашла 12 подходящих паролей
Как видите, они оказались очень простыми

Скорость брутфорса сильно зависит от длины паролей и количества допустимых символов в них, а также от скорости компьютера, на котором проводится процесс взлома. К тому же, брутфорс не проводится «вслепую». Есть списки самых популярных паролей, которые проверяются в первую очередь.

Так что же мешает взломщику просто перебрать все пароли и взломать вашу почту, аккаунты в социальных сетях и все остальное? В теории, остановить его не может ничего, но есть способы очень, очень сильно замедлить процесс взлома, сделав его невыгодным.

Например, после нескольких неправильных попыток ввода пароля добавляются временные задержки перед следующей попыткой или показывается специальная задача, которую могут выполнить только люди — капча.

Различные способы препятствования брутфорсу
Способов много, а цель одна — замедлить взлом

Все эти способы не дают перебирать пароли быстро — десятками тысяч в секунду, невероятно растягивают процесс. Зачем кому-то 10 лет взламывать пароль от вашей электронной почты, если вы за это время либо поменяете пароль, либо вообще смените почту?