Физические величины и вектора

Вводим основным термины, необходимые для дальнейшего изучения физики.

Физические величины

Физическая величина – то, что можно измерить (время, масса и т.д.)

Единица физической величины – то, в чем измеряется физическая величина (килограммы, граммы и т.д.)

Измерительный прибор – то, чем можно измерить физическую величину (весы, секундомер и т.д.)

Рассмотрим для более детального понимания следующую задачу:

Что есть что?

Распределите понятия на группам: «Физическая величина», «Единица физической величины», «Измерительный прибор».

Весы
Транспортир
Градус
Линейка
Сантиметр
Масса
Час
Сутки

Решение

Для начала ответим на вопрос: Что из вышеперечисленнного можно измерить?

Из нашего перечня измерить можно только массу (то есть, например, корректно будет сказать масса равна 2 ..., но некорректно, например, линейка равна 5...). Таким образом, только масса является физической величиной.

Далее найдем все единицы измерения. Для единиц измерения основной вопрос имеет вид: В чем можно что-то измерять?

В нашем случае измерять что-либо можно только в градусах, в сантиметрах и в сутках.

Наконец, прибором является то, при помощи чего мы можем что-то измерить.

В нашем списке, это весы, транспортир, линейка и часы.

Скаляры и вектора

В физике величины делят на скалярные и векторные.

Скалярная физическая величина — величина, характеризующаяся только величиной (числом). Примеры: время, масса, температура и т.д.

Векторная физическая величина — величина, характеризующаяся величиной и направлением. Примеры: сила, скорость, импульс и т.д.

Важной характеристикой векторной величины является проекция вектора на ось.

Термин проекция имеет смысл только для векторных, но не для скалярных физических единиц!

Проекция вектора на ось определяется следующим образом:

Если вектор перепендикулярен оси (вектор w на рисунке), то проекция равна 0 ( $w_x = 0$ )
Если вектор направлен в ту же сторону, что и ось, то проекция вектора равна его длине (модулю) ( $u_x = u$ )
Если вектор направлен в сторону, противоположную оси, то проекция вектора равна его длине (модулю) со знаком минус ( $v_x =-v$ )
Если вектор направлен под некоторым углом $\alpha$ к положительному направлению оси, то проекция вектора равна его длине, умноженной на косинус данного угла ( $a_x =a*\cos\alpha$ )
Если вектор направлен под некоторым углом $\alpha$ к отрицательному направлению оси, то проекция вектора равна его длине со знаком минус и умноженной на косинус данного угла ( $b_x =-b*\cos\alpha$ )

Действия с векторами

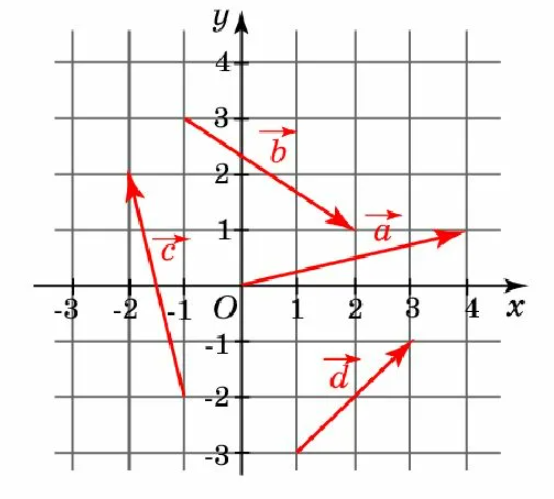
Координатами двумерного вектора называется пара чисел, соответствующих проекциям вектора на 2 перпендикулярные оси Ox и Oy.

Так, например, вектор $\vec{a}$ на рисунке имеет координаты (4; 0), а вектор $\vec{b}$ - координаты (3; -2). Также часто встречается запись через равенство: $\vec{a} = (4; 0); \ \vec{b} = (3; -2)$ .

При сложении векторов их координаты складываются. Так, например, координаты вектора $\vec a + \vec b = (4;0) + (3;-2) = (4+3; 0+(-2)) = (7; -2)$ . Аналогично определяется любая комбинация векторов. Разобраться в этом поможет следующий пример:

Поработаем с векторами

Для векторов, изображенных на рисунке выше:

а) Найдите координаты векторов $\vec{c}$ и $\vec{d}$ ;

б) Найдите координаты векторов $\vec{c} + \vec{d}$ и $\vec{c} - \vec{d}$ ;

в) Найдите координаты векторов $3\cdot\vec{c}$ , $-2\cdot\vec{d}$ и $0,5\cdot\vec{d}$ ;

г) Найдите координаты вектора $2\cdot\vec{c} - 3\cdot\vec{d}$ .

а)

Заметим, что вектор $\vec{c}$ направлен на 1 единицу влево и на 4 единицы вверх, откуда $\vec{c} = (-1; 4)$ .

Аналогично, вектор $\vec{d}$ направлен на 2 единицы вправо и на 2 единицы вверх, откуда $\vec{d} = (2; 2)$ .

б)

$\vec{c} + \vec{d} = (-1; 4) + (2; 2) = (-1 + 2; 4 + 2) = (1; 6)$

$\vec{c} - \vec{d} = (-1; 4) - (2; 2) = (-1 - 2; 4 - 2) = (-3; 2)$

в)

$3\cdot\vec{c} = 3\cdot(-1; 4) = (3\cdot(-1); 3\cdot4) = (-3; 12)$

$-2\cdot \vec{d} = -2\cdot(2; 2) = (-2\cdot 2; -2\cdot2) = (-4; -4)$

$0,5\cdot \vec{d} = 0,5\cdot(2; 2) = (0,5\cdot 2; 0,5\cdot2) = (1; 1)$

г)

$2\cdot\vec{c} - 3\cdot\vec{d} = 2\cdot (-1; 4) - 3 \cdot (2; 2) = (-2; 8) - (6; 6) = (-8; 2)$

Скалярное произведение

Ранее мы рассмотрели, как складывать, вычитать векторы между собой, а также как умножать вектор на число. Однако в математике есть возможность умножать вектора друг на друга, при этом результат будет являться числом!

Скалярное произведение – величина, равная произведению длин векторов на косинус угла между ними:

\vec{a} \cdot \vec{b} = |\vec{a}|\cdot|\vec{b}|\cdot\cos \alpha

Скалярное произведение можно рассчитать, зная только координаты векторов. Для этого используется формула

\vec{a} \cdot \vec{b} = a_x \cdot b_x + a_y \cdot b_y

Отсюда есть несколько важных следствий:

Свойства скалярного произведения

а) (о модуле вектора) Модуль вектора $\vec{a}$ можно вычислить по формуле $|\vec{a}| = \sqrt{\vec a \cdot \vec a}$

б) (об угле между векторами) Угол между векторами $\vec{a}$ и $\vec{b}$ можно вычислить по формуле $\alpha = \arccos(\frac{\vec a \cdot \vec b}{\sqrt{\vec a \cdot \vec a}\cdot \sqrt{\vec b \cdot \vec b}})$

в) (условие перпендикулярности векторов ) Вектора $\vec{a}$ и $\vec{b}$ перпендикулярны тогда и только тогда, когда $\vec{a} \cdot \vec{b} = 0$

Доказательство пункта а)

По определению, $\vec a \cdot \vec a = |\vec a||\vec a|*\cos 0 \degree = |\vec a|^2$ , откуда следует требуемое утверждение

Доказательство пункта б)

По определению, $\vec a \cdot \vec b = |\vec a||\vec b|*\cos \alpha$ , откуда $\alpha = \arccos \frac{\vec a \cdot \vec b}{|\vec a||\vec b|}$ . Послде подстановки выражения для модулей из пункта а) непосредственно получаем требуемое утверждение

Доказательство пункта в)

Заметим, что $90 \degree = arccos(0)$ . Из пункта б) можно заметить, что $\alpha = 90 \degree$ тогда и только тогда, когда равен 0 числитель выражения, то есть при $\vec{a} \cdot \vec{b} = 0$

Рассмотрим задачу на скалярное произведение.

Скалярное произведение

На рисунке приведены несколько векторов.

Найдите скалярное произведение векторов $\vec{a} \cdot \vec {c}$ , длины векторов $\vec a$ и $\vec с$ и угол между ними.

Решение

Из рисунка находим, что $\vec a = (4; 1)$ ; $\vec с = (-1; 4)$ .

Тогда $\vec{a} \cdot \vec {c} = 4\cdot(-1)+1\cdot 4 = -4 + 4 = 0$ ;

$|\vec a| = \sqrt{4^2+1^2} = \sqrt{17}; |\vec c| = \sqrt{(-1)^2+4^2} = \sqrt{17}$ ;

$\alpha = \arccos \frac{\vec a \cdot \vec b}{|\vec a||\vec b|} = \arccos \frac{0}{\sqrt{17}\cdot\sqrt{17}} = 90 \degree$

Упрощение выражений со скалярным произведением

В некоторых задачах бывает необходимо предварительно преобразовывать выражение, содержащее скалярное произведение. Заметим, что для скалярного произведения характерны те же свойства, что и для обычного произведения:

$\vec a \cdot (\vec b + \vec c) = \vec a \cdot \vec b + \vec a \cdot \vec c$

$K \vec a \cdot (L \vec b) = (K\cdot L)(\vec a \cdot \vec b)$

Неизвестное через неизвестное

Чему равна длина вектора $\vec c = 2\vec a + 3\vec b$ , если длина вектора $\vec a$ равна 3, длина вектора $\vec b$ равна 5, а угол между ними равен $120 \degree$ ?

Решение

Сначала найдем квадрат длины искомого вектора:

|\vec c|^2 = \vec c \cdot \vec c = (2\vec a + 3\vec b)^2 = 4\vec a^2 + 12\vec a\vec b + 9\vec b^2

Но $\vec a^2 = |\vec a|^2 = 9; \qquad \vec b^2 = |\vec b|^2 = 25$ ;

$\vec v = |\vec{a}|\cdot|\vec{b}|\cdot\cos \alpha = 3\cdot5\cdot(-0,5)=-7,5$ , откуда

|\vec c|^2 = 4\cdot9+12\cdot(-7,5)+9\cdot 25 = 171 \Rightarrow |\vec c| = \sqrt{171}.

Теперь рассмотрим один пример из физики:

Перпендикулярный полет

Небольшим шариком выстрелили из катапульты со скоростью 𝑣_0 = 15 м/с в вакуумной камере, и спустя время 𝑡 = 1.7 с после выстрела скорость шарика оказалась перпендикулярна начальной. Считая, что скорость изменяется согласно уравнению $\vec v = \vec {v_0} + \vec g t$ , где $𝑔 = 10 м/с^2$ - ускорение свободного падения, найдите величину скорости шарика в этот момент времени.

Решение

Заметим, что условие перпендикулярности $\vec v$ и $\vec v_0$ можно записать в виде $\vec v \cdot \vec v_0 = 0$ .

Но тогда

0 = (\vec v_0 + \vec g t)\vec v_0 = v_0^2 + \vec g \vec v_0 t \Rightarrow \vec g \vec v_0 = -\frac{v_0^2}{t}

Тогда

|\vec v|^2 = \vec v \cdot \vec v = (\vec v_0 + \vec g t)^2 = v_0^2 + 2\vec v_0\vec g t + g^2t^2 = v_0^2-2v_0^2+g^2t^2=g^2t^2-v_0^2=17^2-15^2 = 64

и $v = 8$ м/сек.