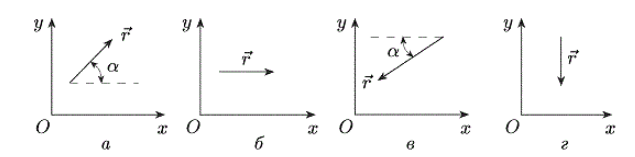
Физические величины и вектора
Физические величины
Разделяй и властвуй!
Выберите из списка все физические величины, единицы измерения и измерительные приборы:
амперметр
ватт
сила тока
энергия
дозиметр
кулон
микроскоп
джоуль
ускорение
Вспомните теорию
Рассмотрите решение подобной задачи.
3, 4, 9 - физические величины
2, 6, 8 - единицы измерения
1, 5, 7 - измерительные приборы
А был ли вектор?
Выберите из списка все векторные физические величины:
мощность
сила
скорость
энергия
работа
температура
перемещение
путь
угол
Вспомните теорию.
Векторные величины: 2, 3, 7
Действия с векторами
Больше векторов богу векторов!
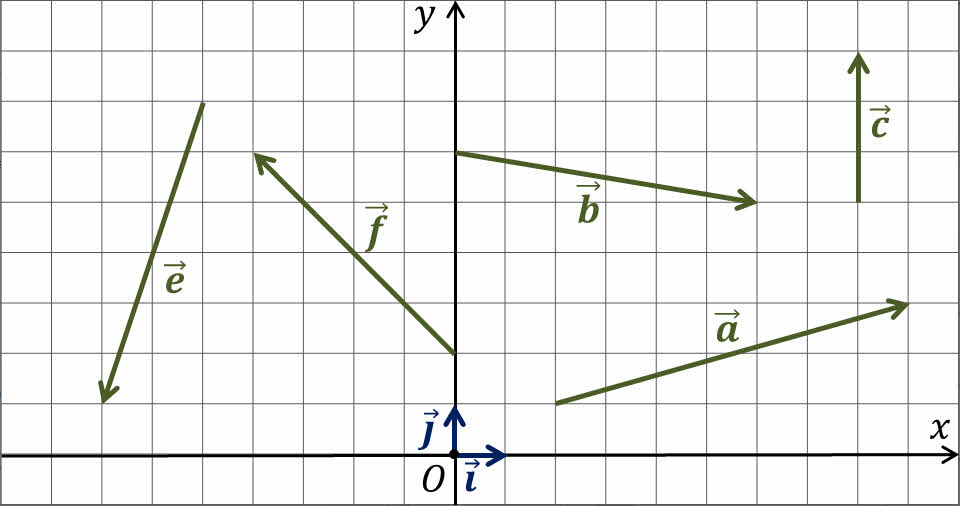
На рисунке изображено несколько векторов.
Найдите координаты всех векторов на рисунке
Найдите координаты вектора
Вспомните теорию.
При сложении векторов их координаты складываются, при вычитании вычитаются
Рассмотрите решение подобной задачи
Легким движением руки вектор превращается... в скаляр
Вспомните теорию.
Кординаты векторов можете взять из предыдущей задачи
Рассмотрите решение подобной задачи
Упрощение выражений со скалярным произведением
Вектор из векторов
Найдите косинус угла между векторами и , если угол между векторами и равен , , .
Рассмотрите решение подобной задачи
Задачу удобно решать по частям: сперва найти длину каждого из векторов, а затем скалярное произведение.
Вектора в физике
Перемещение тела, брошенного под углом к вектору , определяется уравнением . Найти дальность полета тела, то есть перемещение тела в момент, когда .
Рассмотрите решение подобной задачи
Заметим, что .
Тогда .
Но .
Тогда .