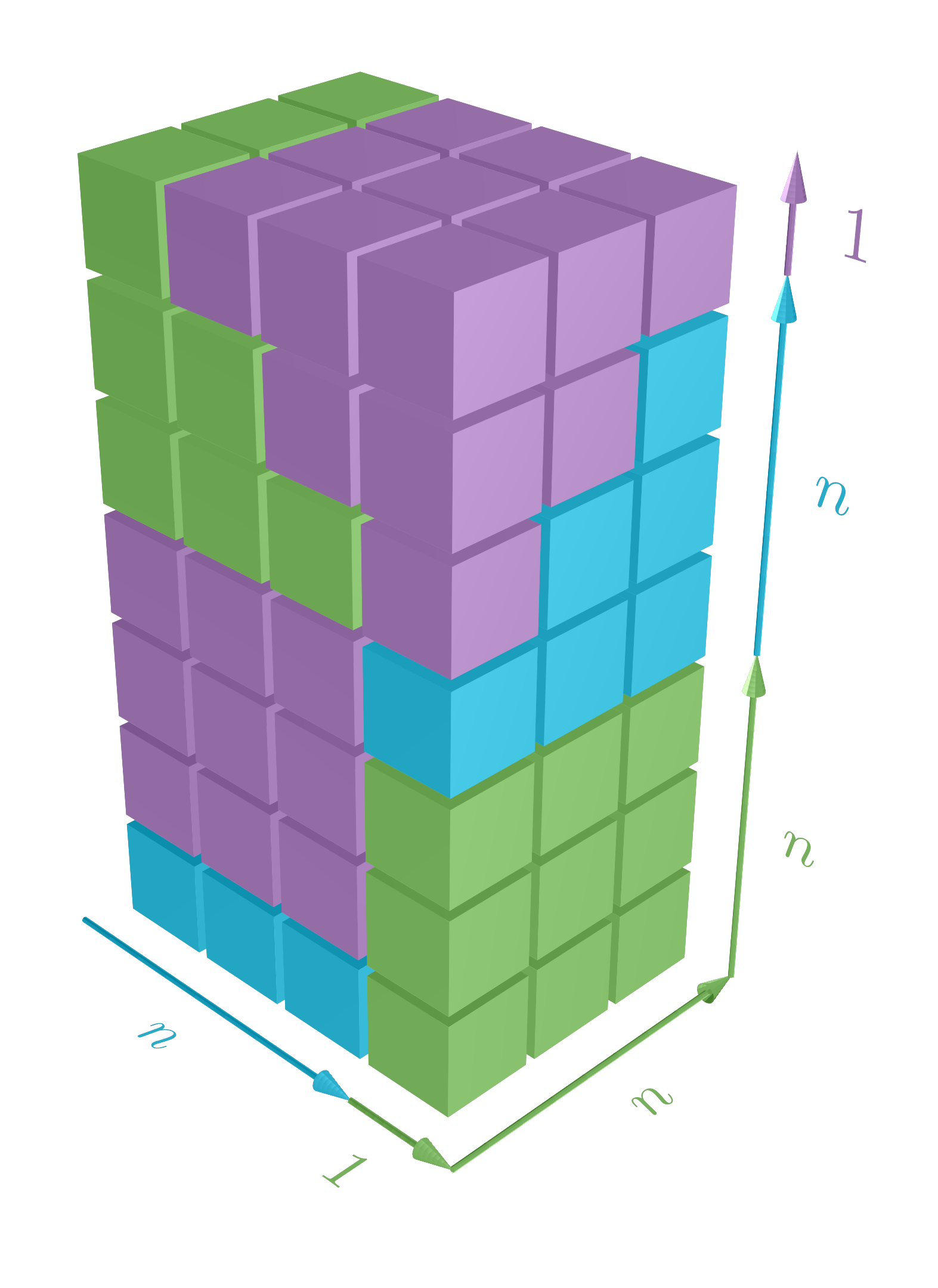
Сумма степеней чисел

Суммы чисел, суммы квадратов, суммы кубов... Разберемся, как можно быстро считать такие суммы. Вы удивитесь, насколько часто они встречаются в самых необычных ситуациях!

Продвинутый уровень

Зависимости

Такие разные суммы...

В математике регулярно приходится иметь дело с самыми разными суммами натуральных чисел в разных степенях:

1 + 2 + 3 + \ldots + n \\ 3^2 + 4^2 + 5^2 + \ldots + 50^2 \\ 8^3 + 10^3 + 12^3 + \ldots + 20^3

Может возникнуть вопрос, а зачем их считать? Дело в том, что подобные суммы встречаются в самых разных разделах математики, в особенности в геометрии. Поверьте, вы даже не представляете, какие замечательные результаты можно получить с их помощью!

Поэтому у математиков возник вопрос — а можно ли как-то быстро посчитать, чему эти суммы равны, без необходимости долго и утомительно возводить в степень и складывать? Ответу на этот вопрос посвящена эта тема.

Записывать такие суммы довольно долго. Чтобы не тратить время и не путаться, введем обозначение $S_n^k$ , обозначающее сумму k-ых степеней первых n натуральных чисел:

Сумма степеней чисел

S^k_n = 1^k + 2^k + 3^k + \ldots + n^k

Использование обозначения

Немного поупражняемся с введенным обозначением для сумм степеней чисел:

S^0_3 = \ ? \qquad S^1_5 = \ ? \qquad S^2_{10} = \ ? \qquad S^k_8 = \ ? \qquad S^3_n = \ ?

Решение

S^0_3 = 1^0 + 2^0 + 3^0 \\ S^1_5 = 1 + 2 + 3 + 4 + 5 \\ S^2_{10} = 1^2 + 2^2 + 3^2 + \ldots + 10^2 \\ S^k_8 = 1^k + 2^k + 3^k + \ldots + 8^k \\ S^3_n = 1^3 + 2^3 + 3^3 + \ldots + n^3

В этой теме мы попытаемся найти прямые и удобные формулы для рассчета произвольных $S_n^k$ — сумм натуральных чисел в любой степени.

Поехали!

Сумма единиц

Начнем с сумм вида $S_n^0$ , то есть сумм первых n натуральных чисел в нулевой степени:

S_n^0 = 1^0 + 2^0 + 3^0 + \ldots + n^0 = \ ?

Как мы помним, любое число в нулевой степени (кроме 0) равно 1. Меняем все числа на единицу и пытаемся решить сложнейшую математическую задачу — найти сумму n единиц:

S_n^0 = \underbrace{1 + 1 + 1 + \ldots + 1}_{n} = \ ?

Тут нам на помощь спешит определение натурального числа, которое само по себе и является суммой единиц. Сумма двух единиц это число 2. Трех — 3. Сумма n единиц — число n.

Сумма единиц

\underbrace{1 + 1 + \ldots + 1}_{n} = n \\ \boxed{S_n^0 = n}

Ах, если бы и остальные суммы считались так же просто...
К сожалению, в этой теме чем дальше, тем сложнее...
Но мы справимся!

Сумма натуральных чисел

Первое серьезное испытание на нашем пути — найти сумму первых n натуральных чисел:

S_n^1 = 1 + 2 + 3 + \ldots + n = \ ?

Такие суммы периодически встречаются в самых разных разделах математики. Одно интересное применение мы рассмотрим тут, а другие дожидаются вас в практикуме.

Но сначала надо разбраться, а как такие суммы вообще считать!

Гениальное решение

Согласно легенде, 8-летний Карл Гаусс плохо себя вел на уроке. Чтобы чем-то надолго занять непослушного мальчишку, учитель дал ему сложную задачу — найти сумму первых 100 натуральных чисел:

1 + 2 + 3 + 4 + \ldots + 100 = \ ?

Устный счёт. В народной школе С. А. Рачинского
Картина Н.П. Богданова-Бельского

План по отвлечению с треском провалился. Маленький гений решил эту задачу меньше чем за минуту и озвучил правильный ответ — 5050. Как он это сделал?! 🤯
Давайте разбираться.

Выпишем в один ряд числа от 1 до 100, а под ним еще один ряд тех же чисел, но в обратном порядке — от 100 до 1. Если складывать верхнее и нижнее числа в каждом столбике, то каждый раз будет получаться число 101!

\def\arraystretch{1.25} \begin{array}{} 1 & 2 & 3 & \ldots & 98 & 99 & 100 \\ + & + & + & + & + & + & + \\ 100 & 99 & 98 & \ldots & 3 & 2 & 1 \\ \hline 101 & 101 & 101 & \ldots & 101 & 101 & 101 \end{array}

Всего 100 столбцов, каждый из которых равен 101. В сумме получаем $100 \cdot 101$ . Но сложив друг с другом столбцы, мы сложили все числа от 1 до 100 дважды:

100 \cdot 101 = \\ = (1 + 100) + (2 + 99) + (3 + 98) + \ldots = \\ = \underbrace{(1 + 2 + 3 + \ldots + 100)}_{\small\text{Сумма 1}} + \underbrace{(100 + 99 + 98 + \ldots + 1)}_{\small\text{Сумма 2}}

Получается, дважды сложив все числа от 1 до 100 мы 100 раз получили число 101:

2 \cdot (1 + 2 + 3 + \ldots + 100) = 100 \cdot 101

Делим обе части равенства на 2 и получаем ответ на задачу:

1 + 2 + 3 + \ldots + 100 = \frac{100 \cdot 101}{2} = 5050

Вот так вот просто можно получить ответ на казалось бы долгую и утомительную вычислительную задачу! Достаточно просто поиграться с суммами чисел и заметить интересный факт, что и сделал маленький Гаусс. Удивлять все математическое сообщество невероятными результатми будущий «король математики» будет на протяжении всей своей жизни...

Тот же самый алгоритм действий можно повторить для суммы любого количества чисел. Дважды сложив n первых натуральных чисел мы n раз получим число $(n+1)$ :

1 + 2 + 3 + \ldots + n = \frac{n(n+1)}{2}

Геометрическое решение

Найти формулу суммы первых n натуральных чисел можно и чисто из геометрических соображений. Для этого каждое число представим в виде синих квадратов, из которых построим «треугольник». Количество квадратов в этом треугольнике и будет равно искомой сумме чисел.

Но как найти, из скольких квадратов мы построили треугольник? Нужно этот треугольник достроить до прямоугольника. Будем делать это зелеными квадратами. Для получения прямоугольника их потребуется столько же сколько и синих:

Получили прямоугольник из n квадратов в ширину и $n+1$ квадрата в длину. Его площадь $n\cdot(n+1)$ будет равна количеству всех использованных в строительстве квадратов.

Прямоугольник мы построили из одинакового количества синих и зеленых квадратов. Поделив найденную площадь на 2, мы как раз и найдем количество только синих (или только зеленых) квадратов, а значит и искомую сумму n первых натуральных чисел:

1 + 2 + 3 + \ldots + n = \frac{\green{n}\cdot(\blue{n\red{+1}})}{2}

Треугольные числа

Числа, получаемые по выведенной формуле, называют треугольными:

T_n = \frac{n(n+1)}{2}

Свое название они получили как раз из-за того, что геометрически их можно представить в виде квадратов или шаров, из которых выложили «треугольник». Вот первые четыре треугольных числа:

Треугольные числа помогают ответить на множество самых разных вопросов. Например, на складе бревен достаточно места, чтобы выложить на земле 22 бревна друг рядом с другом. Какое максимальное количество бревен можно хранить на таком складе?

Бревна надо укладывать в форме треугольника, иначе они укатятся. Поэтому ответом на вопрос будет треугольное число $T_{22} = 253$ . Итак, максимум 253 бревна можно хранить на складе.

Алгебраическое решение

Это решение поначалу может показаться непонятным и запутанным, но обязательно разберитесь в нем! В конечном итоге, когда закончатся геометрические аналогии и гениальные озарения, останется только этот вариант решения!

Начнем со следующего равенства, в котором мы используем формулу квадрата разности:

(n-1)^2 = n^2 - 2n + 1

Обратите внимание, что в правой части есть число n во всех степенях: $n^2, \ n^1$ и даже $n^0 = 1$ . Выпишем подобные разложения квадрата разности для всех чисел от 1 до n:

(1-1)^2 = \blue{1^2} - 2\cdot \blue{1} + \blue{1} \\ (2-1)^2 = \blue{2^2} - 2\cdot \blue{2} + \blue{1} \\ (3-1)^2 = \blue{3^2} - 2\cdot \blue{3} + \blue{1} \\ \ldots \\ (n-1)^2 = \blue{n^2} - 2\cdot \blue{n} + \blue{1}

Посмотрите, как столбики синих чисел образуют цепочки чисел во всех степенях. Теперь сложим все эти равенства друг с другом (отдельно левые и отдельно правые части), вынося за скобки -2:

(1-1)^2 + (2-1)^2 + \ldots + (n-1)^2 = \\ = (1^2 + 2^2 + \ldots + n^2) -2 (1 + 2 + \ldots + n) + (1 + 1 + \ldots + 1)

Обратите внимание, что слева и в скобках справа у нас образовались суммы чисел в разных степенях!

\underbrace{1^2 + 2^2 + \ldots + (n-1)^2}_{\small S_{n-1}^2} = \\ = \underbrace{(1^2 + 2^2 + \ldots + n^2)}_{\small S_n^2} -2 \underbrace{(1 + 2 + \ldots + n)}_{\small S_n^1} + \underbrace{(1 + 1 + \ldots + 1)}_{\small{S_n^0}}

Заменяем длинные суммы на введенное обозначение для сумм степеней чисел:

S_{n-1}^2 = S_n^2 -2 S_n^1 + S_n^0

Красивое получилось равенство...
В него как-бы впечатаны суммы n чисел во всех степенях от 0 до 2.

Ранее мы уже выяснили, что $S_n^0$ равно n. Производим замену, а также изолируем сумму $S_n^1$ , ведь именно ее мы и ищем:

S_n^1 = \frac{1}{2}\left( S_n^2 - S_{n-1}^2 + n \right)

Осталось только найти, чему равна разность $S_n^2 - S_{n-1}^2$ . Довольно очевидно, что если из суммы квадратов от 1 до n вычесть сумму квадратов от 1 до $(n-1)$ , то в итоге останется только $n^2$ .

Вот мы и вывели чисто алгебраически прямую формулу суммы первых n натуральных чисел:

S_n^1 = \frac{1}{2}(n^2 + n) = \frac{1}{2}n^2 + \frac{1}{2}n = \frac{n(n+1)}{2}

Обратите внимание, у нас получилось два ответа: один в виде многочлена, а второй запакованный в виде удобной формулы. Вариант в виде многочлена удобен для анализа и вывода дальнейших формул. Запакованный вариант проще запомнить.

Сумма натуральных чисел

1 + 2 + 3 + \ldots + n = \frac{n(n+1)}{2}

В виде многочлена:

S_n^1 = \frac{1}{2}n^2 + \frac{1}{2}n

Сумма чисел, но не первых!

Найдите, чему равна следующая сумма чисел:

50 + 51 + 52 + \ldots + 100 = \ ?

А кто сказал, что будет легко?

Решение

Выпишем сумму всех чисел от 1 до 100:

S_{100}^1 = 1 + 2 + 3 + \ldots + 100

Обратите внимание, что ее можно разбить на две подгруппы: сумму чисел от 1 до 49 и сумму оставшихся чисел:

\underbrace{\underbrace{1 + 2 + \ldots + 49}_{\small S_{49}^1} + \underbrace{50 + 51 + \ldots + 100}_{\small \ ?}}_{\small S_{100}^1}

Выходит, искомую сумму чисел от 50 до 100 можно найти, если из «целого» $S_{100}^1$ вычесть «часть» $S_{49}^1$ :

50 + \ldots + 100 = S_{100}^1 - S_{49}^1 = \frac{100 \cdot 101}{2} - \frac{49 \cdot 50}{2} = 3825

Сумма квадратов чисел

Повышаем ставки! Теперь мы будем искать прямую формулу для рассчета суммы квадратов чисел:

S_n^2 = 1^2 + 2^2 + 3^2 + \ldots + n^2 = \ ?

Геометрическое решение

Как сумму обычных чисел можно представить в виде «треугольника», так и сумму квадратов можно изобразить графически — в виде пирамидок из кубиков с квадратными основаниями:

При таком взгляде на проблему искомая сумма будет равна количеству кубов, из которых состоит пирамида. Но как быстро посчитать количество кубов? Нужно попытаться достроить эту пирамиду до простой фигуры, объем которой легко найти. Например, до параллелепипеда.

Сделать это не так-то просто. Но у мыслителей Античности, без интернета и компьютерных игр, было много времени на размышления. В итоге они таки смогли получить параллелепипед, хитрым образом совместив вместе целых шесть одинаковых пирамид!

Построение параллелепипеда из шести пирамид

Отметим размеры (длину, ширину и высоту) параллелепипеда:

Посчитаем его объем, а значит и количество кубов из которых он состоит:

V = \underbrace{n}_{\text{Ширина}} \times \underbrace{(n+1)}_{Длина} \times \underbrace{(2n + 1)}_{\text{Высота}}

Но этот параллелепипед составлен из шести одинаковых пирамид, то есть из шести одинаковых сумм n чисел в квадрате. Значит, для получения одной суммы, надо найденный объем поделить на 6:

1^2 + 2^2 + 3^2 + \ldots + n^2 = \frac{n(n+1)(2n+1)}{6}

Вот так вот геометрия в очередной раз пришла на выручку алгебре! Геометрическое решение хорошо еще и тем, что с его помощью саму формулу легко запомнить: параллелепипед с увеличивающимися сторонами n, $n+1$ , $2n+1$ , делим на 6 одинаковых пирамид, из которых он и состоит.

Квадратные пирамидальные числа

Мы открыли еще один тип так называемых «фигурных» чисел, то есть чисел, которые можно представить в виде геометрических фигур. Числа, получаемые из выведенной нами формулы называются «квадратными пирамидальными».

С этими числами связана сформулированная в 19-м веке «задача о пушечных ядрах»: сколько пушечных ядер можно уложить и в один слой в форме квадрата, и в форме пирамиды с квадратным основанием?

Квадрат можно сформировать из $m^2$ ядер. Формулу количества ядер для постройки пирамиды с квадратным основанием мы тоже уже знаем. Задача сводится к решению следующего уравнения в натуральных числах:

m^2 = \frac{n(n+1)(2n+1)}{6}

Оказывается, исключая тривиальное решение из 1 ядра, у задачи есть только один ответ: $m = 70$ и $n=24$ . Другими словами, только 4900 ядер можно уложить и в квадрат, и в виде квадратной пирамиды!

Алгебраическое решение

Алгоритм вывода точно такой же, как и алгебраический вывод суммы натуральных чисел. Только в этот раз надо выписывать суммы уже в третьей степени. Попробуйте сделать вывод самостоятельно, а потом проверьте себя:

Сумма квадратов

1^2 + 2^2 + 3^2 + \ldots + n^2 = \frac{n(n+1)(2n+1)}{6}

В виде многочлена:

S_n^2 = \frac{1}{3}n^3 + \frac{1}{2}n^2 + \frac{1}{6}n

Доказательство

Выпишем разложения $(n-1)^3$ по формуле куба разности для всех чисел от 1 до n:

(1-1)^3 = \blue{1^3} - 3\cdot \blue{1^2} + 3\cdot \blue{1} - \blue{1} \\ (2-1)^3 = \blue{2^3} - 3\cdot \blue{2^2} + 3\cdot \blue{2} - \blue{1} \\ (3-1)^3 = \blue{3^3} - 3\cdot \blue{3^2} + 3\cdot \blue{3} - \blue{1} \\ \ldots \\ (n-1)^3 = \blue{n^3} - 3\cdot \blue{n^2} + 3\cdot \blue{n} - \blue{1}

Складываем все эти равенства и используем введенное обозначение для сумм:

S_{n-1}^3 = S_n^3 -3 S_n^2 + 3 S_n^1 - S_n^0

Изолируем искомую сумму $S_n^2$ :

S_n^2 = \frac{1}{3}\left(S_n^3 - S_{n-1}^3 + 3S_n^1 - S_n^0\right)

Подставляем уже найденные формулы для сумм $S_n^0$ и $S_n^1$ , а также заменяем разность $S_n^3 - S_{n-1}^3$ на $n^3$ :

S_n^2 = \frac{1}{3}\left( n^3 + \frac{3}{2}n^2 + \frac{3}{2}n - n \right) = \frac{1}{3}n^3 + \frac{1}{2}n^2 + \frac{1}{6}n

Мы получили формулу в виде многочлена. Для получения запакованной формулы как в геометрическом решении приводим все к общему знаменателю и находим корни квадратного уравнения:

\frac{1}{3}n^3 + \frac{1}{2}n^2 + \frac{1}{6}n = \frac{2n^3 + 3n^2 + n}{6} = \frac{n(2n^2 + 3n + 1)}{6} = \frac{n(n+1)(2n+1)}{6}

$\blacksquare$

Первый пропал!

Вычислите следующую сумму:

2^2 + 3^2 + 4^2 + \ldots + 50^2 = \ ?

Решение

С помощью выведенной формулы находим сумму всех квадратов чисел от 1 до 50:

S_{50}^2 = \frac{50 \cdot 51 \cdot 101}{6} = 42 \ 925

Но в нашей задаче сумма начинается с $2^2$ , а не с единицы, поэтому из найденной суммы надо вычесть $1^2$ :

42 \ 925 - 1^2 = 42 \ 924

Сумма кубов чисел

Последняя степень, в которой еще можно получить прямую формулу «элементарным» и наглядным способом. Разберемся же с суммой кубов чисел!

S_n^3 = 1^3 + 2^3 + 3^3 + \ldots + n^3 = \ ?

Гениальная гипотеза

Сейчас речь пойдет не о решении, а о гипотезе. Ее плюс в том, что она очень легко запоминается и выводится, а минус в том, процесс ее получения не является доказательством — верность полученной формулы придется доказывать отдельно.

Выпишем в первой строке таблицы, чему равны суммы первых натуральных чисел, а во второй суммы их кубов и попробуем найди взаимосвязь:

\def\arraystretch{2} \begin{array}{c|} n & 1 & 2 & 3 & 4 & \ldots & n \\ \hline S_n^1 & 1 & 3 & 6 & 10 & \ldots & \dfrac{n(n+1)}{2} \\ S_n^3 & 1 & 9 & 36 & 100 & \ldots & ? \end{array}

Обратили внимание, что сумма кубов в точности равна квадрату суммы обычных чисел?

\begin{array}{} 1^1 = 1 && 3^2 = 9 && 6^2 = 36 && 10^2 = 100 \end{array}

Может возникнуть предположение, что вообще любая сумма кубов n чисел будет равна квадрату суммы этих же n чисел. И это предположение действительно верное:

1^3 + 2^3 + \ldots + n^3 = \left(1 + 2 + \ldots + n\right)^2 = \\ = \left(\frac{n(n+1)}{2}\right)^2 = \frac{n^2(n+1)^2}{4}

Теорема Никомаха

На самом деле даже формулу суммы кубов можно «вывести» геометрически. Просто делается это уже не так элементарно, наглядно и естественно, и к тому же задействует «разрезание» фигур:

Представляем кубы чисел в виде геометрических кубов, нарезаем их на слои. Причем последний слой каждого четного куба нужно дополнительно разрезать надвое.

Из полученных слоев выкладываем большой квадрат со стороной, равной сумме чисел $1 + 2 + \ldots$ Его площадь $(1+2+\ldots)^2$ и равна количеству всех использованных кубиков:

1^3 + 2^3 + \ldots = (1+2+\ldots)^2 = \frac{n^2(n+1)^2}{4}

Это равенство иногда называют теоремой Никомаха в честь древнегреческого математика Никомаха Герасского (II век нашей эры).

Алгебраическое решение

Гипотеза может выглядеть сколь угодно соблазнительно, но использовать ее без доказательства опасно. К счастью, у нас уже есть рабочий метод вывода прямых формул для сумм степеней чисел:

Сумма кубов

1^3 + 2^3 + 3^3 + \ldots + n^3 = \frac{n^2(n+1)^2}{4}

В виде многочлена:

S_n^3 = \frac{1}{4}n^4 + \frac{1}{2}n^3 + \frac{1}{4}n^2

Доказательство

Повторяем точно такие же действия, как и при выводе сумм квадратов.

Для строгого вывода формулы нам нужно найти разложение $(n-1)^4$ . Сделать это можно двумя способами: долго и муторно умножать скобоки вручную или задействовать бином Ньютона. Именно его и используем:

(n-1)^4 = C_4^0 n^4 - C_4^1 n^3 + C_4^2 n^2 - C_4^3 n + C_4^4

Считаем биномиальные коэффициенты либо по формуле сочетаний, либо через треугольник Паскаля:

(n-1)^4 = n^4 - 4n^3 + 6n^2 - 4n + 1

Суммируем это равенство для всех чисел от 1 до n и полученные суммы заменяем на введенные обозначения:

S_{n-1}^4 = S_n^4 -4 S_n^3 + 6S_n^2 - 4S_n^1 + S_n^0

Пользуемся равенством $S_n^4 - S_{n-1}^4 = n^4$ :

0 = n^4 -4 S_n^3 + 6S_n^2 - 4S_n^1 + S_n^0

Изолируем искомую сумму $S_n^4$ и подставляем уже полученные ранее прямые формулы для сумм чисел:

S_n^3 = \frac{1}{4}\left( n^4 + \frac{6}{3}n^3 + \frac{6}{2}n^2 + \frac{6}{6}n - \frac{4}{2}n^2 - \frac{4}{2}n + n \right) = \frac{1}{4}\left( n^4 + 2n^3 + n^2 \right) = \frac{1}{4}n^4 + \frac{1}{2}n^3 + \frac{1}{4}n^2

Получили формулу в виде многочлена. Для получения запакованного варианта приводим к общему знаменателю, выносим за скобки $n^2$ и применяем формулу квадрата суммы на оставшейся скобке:

\frac{1}{4}n^4 + \frac{1}{2}n^3 + \frac{1}{4}n^2 = \frac{n^4 + 2n^3 + n^2}{4} = \frac{n^2(n^2 + 2n + 1)}{4} = \frac{n^2(n+1)^2}{4}

$\blacksquare$

Кубическая сумма

Вычислите следующую сумму:

1^3 + 2^3 + 3^3 + \ldots + 25^3 = \ ?

Решение

Используем выведенную формулу:

S_{25}^3 = \frac{25^2 \cdot 26^2}{4} = 105 \ 625

Проблема больших степеней

Мы получили прямые формулы для сумм чисел в степенях от 0 до 3. А что дальше?
А дальше начинаются большие проблемы...

Геометрический подход перестает работать. Для простой суммы чисел в первой степени мы задействовали площадь. Для суммы квадратов задействовали объем. Чтобы продвинуться дальше нужно либо выходить в многомерные пространства, что наши мозги очень плохо умеют делать, либо выдумывать какие-то очень сложные геометрические аналогии.

Хитрые приемы и озарения тоже закончились. Слишком сложные получаются формулы. Их не вывести каким-то необычным и простым действием, по типу попарного сложения противоположных чисел (как в решении Гаусса) или возведения в квадрат (как в сумме кубов).

Вот и получается, что два самых любимых метода ученых древности (геометрия и необычные ходы) перестали работать. Алгебра же в те времена была крайне слабо развита. Из-за этого вся история с суммами степеней чисел зашла в тупик и простаивала без малого 1000 лет!

И только в 17-м веке, с развитием алгебры, ученым удалось полностью разобраться в этом вопросе и получить алгоритмы вывода прямых формул для любой степени, без привязки к алгебре или каким-то нестандартным фактам.

Рекуррентная формула

Каждый раз, когда речь заходит о степенях и длинных суммах, это повод задуматься о биноме Ньютона. Он часто выступает своеобразным «мостиком» между суммами и их общими формулами.

Сейчас мы будем обобщать на произвольные степени единственный оставшийся у нас рабочий способ вывода формул — алгебраический. Если у вас возникнут сложности, то сначала самостоятельно выведите уже описанные выше формулы для первой, второй и третьей степеней алгебраическим способом.

Рассмотрим разложение следующей степени бинома:

(n-1)^{k+1} = C_{k+1}^0 \ \blue{n^{k+1}} - C_{k+1}^1 \ \blue{n^{k}} + C_{k+1}^2 \ \blue{n^{k-1}} - \ldots + (-1)^{k+1}C_{k+1}^{k+1} \ \blue{n^{0}}

Обратите внимание, что в разложении встречаются все степени числа n от k-ой, до нулевой. Выпишем все возможные разложения чисел от 0 до n:

(1-1)^{k+1} = C_{k+1}^0 \ \blue{1^{k+1}} - C_{k+1}^1 \ \blue{1^{k}} + C_{k+1}^2 \ \blue{1^{k-1}} - \ldots + (-1)^{k+1}C_{k+1}^{k+1} \ \blue{1^{0}} \\ (2-1)^{k+1} = C_{k+1}^0 \ \blue{2^{k+1}} - C_{k+1}^1 \ \blue{2^{k}} + C_{k+1}^2 \ \blue{2^{k-1}} - \ldots + (-1)^{k+1}C_{k+1}^{k+1} \ \blue{2^{0}} \\ (3-1)^{k+1} = C_{k+1}^0 \ \blue{3^{k+1}} - C_{k+1}^1 \ \blue{3^{k}} + C_{k+1}^2 \ \blue{3^{k-1}} - \ldots + (-1)^{k+1}C_{k+1}^{k+1} \ \blue{3^{0}} \\ \cdots \\ (n-1)^{k+1} = C_{k+1}^0 \ \blue{n^{k+1}} - C_{k+1}^1 \ \blue{n^{k}} + C_{k+1}^2 \ \blue{n^{k-1}} - \ldots + (-1)^{k+1}C_{k+1}^{k+1} \ \blue{n^{0}}

Сложим все эти равенства друг с другом (отдельно левые и отдельно правые части). В правой части выносим за скобки одинаковые биномиальные коэффициенты:

0^{k+1} + 1^{k+1} + 2^{k+1} + \ldots + (n-1)^{k+1} = \\ = C_{k+1}^0(1^{k+1} + \ldots + n^{k+1}) - C_{k+1}^1(1^{k} + \ldots + n^{k}) + \ldots + (-1)^{k+1}C_{k+1}^{k+1}(1^0 + \ldots + n^0)

Теперь заменим сумму в левой части равенства и суммы в скобках в правой части на введенное обозначение сумм степеней чисел:

S_{n-1}^{k+1} = C_{k+1}^0 S_n^{k+1} - C_{k+1}^1 S_n^{k} + \ldots + (-1)^{k+1}C_{k+1}^{k+1}S_n^0

Невероятно! Всего парой простых действий с биномами Ньютона мы получили единую формулу, в которую «впечатаны» все суммы n чисел всех степеней (от 0 до $k+1$ )!

Но нам все же нужна сумма n чисел в k-й степени, а не сумма n чисел $k+1$ -й степени. Поэтому еще немного преобразуем равенство.

Для начала избавимся от сумм $k+1$ -й степени, используя тот факт, что разность $S_n^{k+1} - S_{n-1}^{k+1}$ равна $n^{k+1}$ :

0 = \underbrace{\underbrace{C_{k+1}^0}_{\small 1} S_n^{k+1} - S_{n-1}^{k+1}}_{\small n^{k+1}} -C_{k+1}^1 S_n^k + \ldots + (-1)^{k+1}C_{k+1}^{k+1}S_n^0

0 = n^{k+1} -C_{k+1}^1 S_n^k + \ldots + (-1)^{k+1}C_{k+1}^{k+1}S_n^0

Изолируем искомую сумму $S_n^k$ :

S_n^k = \frac{1}{\underbrace{C^1_{k+1}}_{k+1}} \left( n^{k+1} + C^2_{k+1}S^{k-1}_n - \ldots + (-1)^{k+1}C_{k+1}^{k+1}S_n^0 \right)

Наконец, в правой части равенства используем символ суммы и получаем окончательную формулу:

Рекуррентая формула суммы степеней

S_n^k = \frac{1}{k+1}\left(n^{k+1} + \sum\limits_{t=2}^{k+1} (-1)^t C_{k+1}^t S_n^{k+1-t}\right)

«Рекуррентной» эта формула называется потому что для получения значения $S_n^k$ , нам нужно сначала по этой же формуле вычислить формулы сумм всех предыдущих степеней: $S_n^{k-1}, \ S_n^{k-2}$ и так далее...

Мы получили великолепный результат — доказали, что прямые формулы для суммы чисел любых степеней существуют и даже нашли способ их вывести!

Опробуем формулу в деле!

Покорение четвертой степени!

Найдите прямую формулу для суммы чисел в четвертой степени:

1^4 + 2^4 + 3^4 + \ldots + n^4 = \ ?

С помощью этой формулы посчитайте сумму первых 15 чисел в четвертой степени.

Решение

Пользуемся выведенной рекуррентной формулой:

S_n^4 = \frac{1}{5} \left( n^5 + C^2_5S_n^3 - C^3_5S_n^2 + C^4_5S_n^1 - C^5_5S_n^0 \right)

Считаем биномиальные коэффициенты:

S_n^4 = \frac{1}{5} \left( n^5 + 10 S_n^3 - 10 S_n^2 + 5 S_n^1 - S_n^0 \right)

Подставляем формулы для ранее выведенных сумм, раскрываем скобки и приводим подобные:

\boxed{ S_n^4 = \frac{1}{5}n^5 + \frac{1}{2}n^4 + \frac{1}{3}n^3 - \frac{1}{30}n }

Формула готова! С ее помощью считаем сумму первых 15 чисел в четвертой степени:

S_{15}^4 = \frac{1}{5}\cdot 15^5 + \frac{1}{2}\cdot 15^4 + \frac{1}{3}\cdot 15^3 - \frac{1}{30}\cdot 15 = 178 \ 312

Прямая формула?

Полученной нами рекуррентной формулы вполне достаточно для вывода прямых формул сумм чисел небольших степеней. Но чем выше степень, тем более трудоемким становится процесс вывода.

Есть ли способ попроще? И да и нет. В начале 18-го века Якоб Бернулли получил прямую формулу суммы степеней чисел, без необходимости высчитывать формулы сумм меньших степеней:

S_n^k = \frac{1}{k+1}\sum\limits_{t=0}^k C_{k+1}^t B_t n^{k+1-t}

Эта формула (формула Фаульхабера) очень похожа на нашу рекуррентную. Вот только вместо предыдущих сумм в ней используются особые числа $B_t$ , называемые числами Бернулли. Эти числа появляются во многих других крайне полезных математических формулах, в основном в высшей математике.

Проблема в том, что считаются эти числа тоже по рекуррентной формуле и для вычисления числа $B_i$ , прямо как и с суммами, надо вычислить все предыдущие числа: $B_{i-1}$ , $B_{i-2}$ и так далее вплоть до $B_1$ .

Поэтому да, несколько более простая формула действительно существует, но нет, в ней все равно предостаточно рекуррентных вычислений.